hidden_poly

是一个比较基础的格题，但是我还是一下没做出来...也值得学习记录一下

题目给出的等式即存在 \(k\in\mathbb{Z}\)，使得 \[ \sum_{i=0}^{15}key_{i}*root^{i}+kq=0 \]

常规思路

构造格基即 \[ (key_0,key_1,\dots,key_{15},k) \begin{pmatrix} 1 & 0 & 0 & \dots& 0 & root^0\\ 0 & 1 & 0 & \dots& 0 & root^1\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & \dots& 1 & root^{15}\\ 0 & 0 & 0 & \dots& 0 & q \end{pmatrix} = (key_0,key_1,\dots,key_{15},0) \] 算一下范数，格基是 \(\sqrt {16} q^{\frac{1}{16}}\) 大概 \(10\) 位，而目标向量按最长算也就是 \(\sqrt{(2^7)^2*16}\) 大概 \(9\) 位，是平衡的

但是这里有一个问题，就是这个格基的最短向量不是目标向量，而是这里的第一行向量 \[ \begin{pmatrix} 1 & 0 & 0 & 0 & \dots & root^0 \end{pmatrix} \] \(root^0\) 即 \(1\)，这个向量显然比 \[ (key_0,key_1,\dots,key_{15},0) \] 要短，故规约出来的结果第一个行向量，即最短向量，不是目标向量

规约出来的结果如下

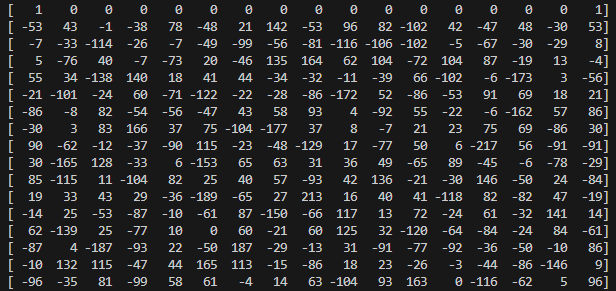
可以看到，第一行向量，即最短向量确实是 \(\begin{pmatrix} 1 & 0 & 0 & 0 & \dots & root^0 \end{pmatrix}\)，所以要往下寻找目标向量

第二行中，出现了值为 \(142\) 的分量，超过了 \(key_i\) 的范围 \(0 \sim 2^7\) ，也不是要找的目标向量

第三行的向量分量全都符合范围，应该就是要找的目标向量

但是这里又出现了一个问题，回看刚才构造的格基和等式，可以看到目标向量的最后一个分量应当是 \(0\)，但是这里并不是 \(0\)，为什么呢？

再次回到等式 \[ \sum_{i=0}^{15}key_{i}*root^{i}+kq=0 \] 展开来写 \[ key_0*root^0+key_{1}*root^{1}+key_{2}*root^{2}+\dots+key_{15}*root^{15}+kq=0 \] 即 \[ key_0+key_{1}*root^{1}+key_{2}*root^{2}+\dots+key_{15}*root^{15}+kq=0 \] 写成这样就能看出来，多出来的值是从哪里来的了：这个多项式只有第一项 \(key_0\) 是在 \(0\sim2^7\) 内，所以其实规约出来的结果，\(key_0\) 的正确值应当是第三行的第一个分量的值减去最后一个分量的值

exp 如下

from Crypto.Util.number import *
from Crypto.Cipher import AES
 
q = 264273181570520944116363476632762225021
root = 122536272320154909907460423807891938232
n = 16
iv = b'Gc\xf2\xfd\x94\xdc\xc8\xbb\xf4\x84\xb1\xfd\x96\xcd6\\'
ciphertext = 'd23eac665cdb57a8ae7764bb4497eb2f79729537e596600ded7a068c407e67ea75e6d76eb9e23e21634b84a96424130e'
ciphertext=bytes.fromhex(ciphertext)

M = Matrix(ZZ, n+1, n+1)
for i in range(n):
    M[i, i] = 1
    M[i, -1] = root^i
M[-1, -1] = q
M = M.LLL()
print(M)

key = [None]*n
for i in range(1,n):
    key[i] = chr(abs(int(M[2][i])))
key[0] = chr(abs(int(M[2][0]-M[2][-1])))
key = ''.join(key)

cipher = AES.new(key.encode(),AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
print(plaintext)

改进思路

既然上面说了，最短的向量是 \(\begin{pmatrix} 1 & 0 & 0 & 0 & \dots & root^0 \end{pmatrix}\)，那么可以直接把它避开

有 \[ key_0+key_{1}*root^{1}+key_{2}*root^{2}+\dots+key_{15}*root^{15}+kq=0 \] 则 \[ key_{1}*root^{1}+key_{2}*root^{2}+\dots+key_{15}*root^{15}+kq=-key_0 \] 构造 \[ (key_1,key_2,\dots,key_{15},k) \begin{pmatrix} 1 & 0 & 0 & \dots& 0 & root^1\\ 0 & 1 & 0 & \dots& 0 & root^2\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & \dots& 1 & root^{15}\\ 0 & 0 & 0 & \dots& 0 & q \end{pmatrix} = (key_1,key_2,\dots,key_{15}, -key_0) \] 这样还把最后一列规约不出来 \(0\) 的问题一并解决了，是一个改进的方法

exp 如下

from Crypto.Cipher import AES
from Crypto.Util.number import *

q = 264273181570520944116363476632762225021
root = 122536272320154909907460423807891938232
n = 16
iv = b'Gc\xf2\xfd\x94\xdc\xc8\xbb\xf4\x84\xb1\xfd\x96\xcd6\\'
ciphertext = 'd23eac665cdb57a8ae7764bb4497eb2f79729537e596600ded7a068c407e67ea75e6d76eb9e23e21634b84a96424130e'
ciphertext=bytes.fromhex(ciphertext)

M = Matrix(ZZ, n, n)
for i in range(n-1):
    M[i, i] = 1
    M[i, -1] = root^(i+1)
M[-1, -1] = q
M = M.LLL()
print(M)

key = []
for i in range(n):
    key.append(chr(abs(int(M[0][i]))))
key = ''.join(key)
key = key[-1]+key[:-1]

cipher = AES.new(key.encode(),AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
print(plaintext)